What is the PAPRIKA method?

Award-winning, patented technology
1000minds’ “secret spice” is the “PAPRIKA” method, which was invented by 1000minds’ founders, Paul Hansen and Franz Ombler, to help people make decisions consistently, fairly and transparently and for discovering what matters to people.
The PAPRIKA method was designed to be as cognitively simple and user-friendly as possible, as well as scientifically valid and reliable. For reasons that will be explained later below, the name “PAPRIKA” is an acronym for the method’s full name: Potentially All Pairwise RanKings of all possible Alternatives.
PAPRIKA has been patented and recognized in 15 innovation awards, including being complimented as “a tool of great power and sheer elegance” (Consensus Software Award 2010, sponsored by IBM and Microsoft).
In addition to business, government and nonprofit users, the PAPRIKA method is used for research and teaching at 550+ universities and other research organizations worldwide. Since 2006, 310+ peer-reviewed articles or abstracts about PAPRIKA applications have been published.
PAPRIKA method
PAPRIKA involves the decision-maker – e.g. you! – answering a series of simple questions based on choosing between two hypothetical alternatives defined on just two criteria or attributes at a time and involving a trade-off between them.
How you answer the questions depends on how you feel, based on your expertise and judgement, about the relative importance of the two criteria/attributes appearing in each question.
The questions are repeated with different pairs of hypothetical alternatives defined on different combinations of the criteria or attributes – hereinafter mostly referred to simply as “criteria” – for your application until your preferences are captured.
Below are two examples of PAPRIKA’s trade-off questions. Figure 1 is in the context of Multi-Criteria Decision Analysis (MCDA), also known as Multi-Criteria Decision-Making (MCDM); and Figure 2 is for conjoint analysis, also known as a discrete choice experiment (DCE). (1000minds is the only software in the world that combines the power of both decision-making and conjoint analysis in one beautiful package.)
Depending on the application, PAPRIKA’s questions can be answered by individual decision-makers working on a decision on their own; or by groups voting on the questions in pursuit of consensus; or by 1000s of participants in a 1000minds preferences survey (especially useful for conjoint analysis).
PAPRIKA’s trade-off questions
PAPRIKA’s trade-off questions have these three fundamental characteristics, which hold in all applications of the method:
- Each question involves a trade-off between the two criteria defining the two alternatives you are asked to choose between. How you answer each question depends on how you feel about the relative importance of the two criteria.
- In each question, any other criteria included in the application but not appearing in the question – e.g. “engine size”, “safety features”, etc for Figure 2’s application – are implicitly treated as the same for the alternatives in the question: i.e. “all else being equal”. These other criteria will appear, two at a time, in other trade-off questions asked by PAPRIKA.
- The two alternatives in each question – e.g. “projects” or “cars” in Figures 1 and 2 above – are hypothetical, or imaginary, instead of being actual alternatives you might be considering. By choosing between hypothetical alternatives, you are expressing your preferences in general terms.
Easiest questions possible
Compared to other methods, the advantage of PAPRIKA’s questions – like Figures 1 and 2 above – is that they involve just two alternatives differentiated on two criteria at a time. They are the easiest possible questions involving trade-offs for you to think about, and therefore you can have confidence in the accuracy of your answers.
Such simple questions are repeated with different pairs of hypothetical alternatives, always involving trade-offs between different combinations of the criteria, two at a time.
When you have finished answering questions with just two criteria – usually taking very little time – it’s possible to go to the “next level of decision-making” by answering questions with three criteria, and then four, etc, up to the number of criteria for your application.
However, answering questions with just two criteria is usually sufficient to accurately reveal your preferences, so that for most applications you can stop after having done so.
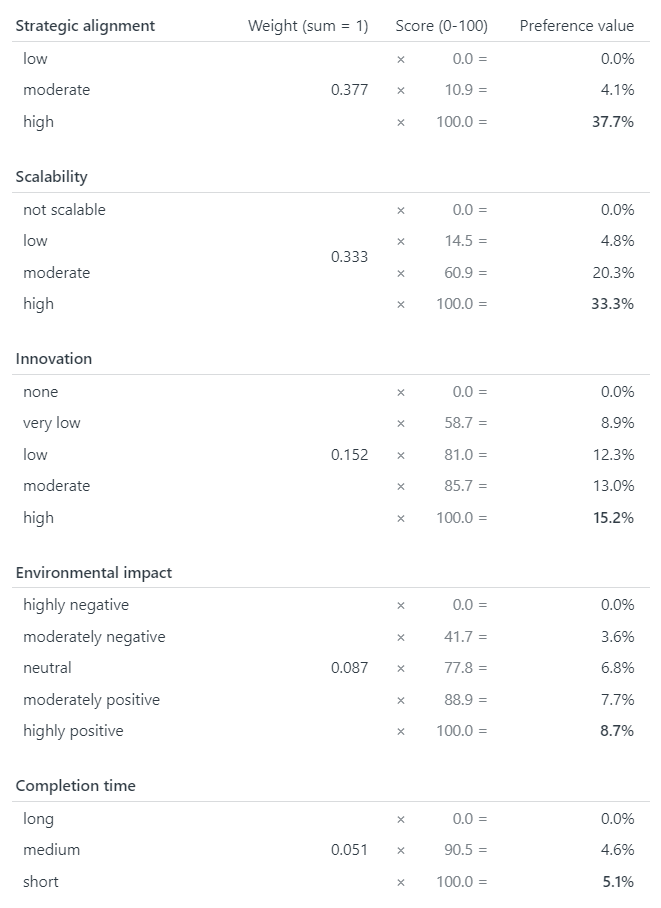
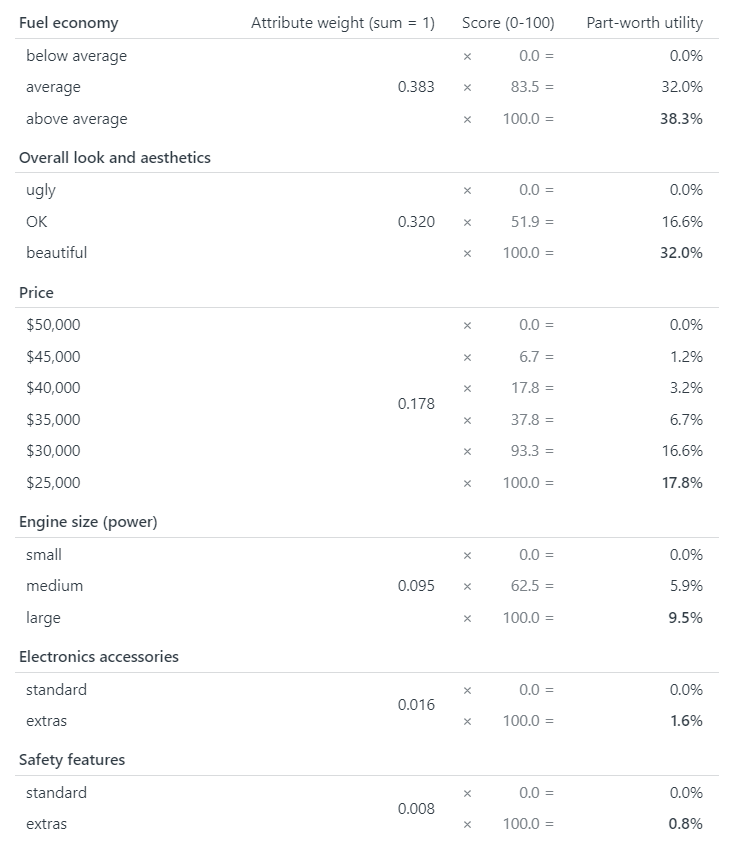
From your answers, PAPRIKA codifies how you feel about the relative importance of the criteria as weights – often referred to as “preference values” or “utilities”, also known as “part-worths”. These weights are used to rank any alternatives you are considering.
Additive and adaptive
Like most methods for decision-making and conjoint analysis, PAPRIKA is based on what are known in the academic literature as additive “multi-criteria value models” or “multi-attribute value models” – also commonly referred to as “weighted-sum”, “additive”, “linear”, “scoring”, “point-count” or “points” models or systems.
As highlighted by these names, the defining characteristic of such models is that the weights on the criteria and their levels are aggregated for each alternative by summing the weights to obtain the alternative’s “total score” – i.e. a weighted-sum, usually in the range 0-100 – by which the alternatives are ranked.
Such models have been found in very many studies to be very accurate (Hastie and Dawes 2010; Kahneman 2011; Kahneman, Sibony & Sunstein 2021).
As well as being based on additive models, PAPRIKA is recognized as a type of adaptive conjoint analysis (ACA), also known as adaptive choice-based conjoint analysis (ACBC) – because PAPRIKA continually adapts as it goes about presenting you with your own personalized sequence of questions, as determined by how you answer them, one-by-one.
Each time you answer a question, PAPRIKA “thinks” for a split second and then, based on your earlier answers, selects the next question to ask you. When you answer it, PAPRIKA thinks again and selects another question for you, and then another, and so on until your preferences have been fully elicited.
PAPIRKA’s objective as it adaptively selects your questions is to minimize how many you are required to answer to arrive at pairwise rankings for all hypothetical alternatives defined on two criteria at a time. Thus, the method is known by its “PAPRIKA” acronym because it results in the identification of Potentially All Pairwise RanKings of all possible Alternatives (PAPRIKA).
How many trade-off questions do you need to answer? The number depends on how many attributes and levels you have for your application and how you answer them.
For example, with four attributes and three or four levels for each attribute, approximately 25 questions would be asked on average – taking most people less than 10 minutes.
No design issues
A major advantage arising from PAPRIKA’s adaptivity is that administrators of conjoint analysis surveys don’t need to worry about specifying the questions to be asked in their surveys – instead, that’s all taken care of by PAPRIKA automatically (via 1000minds’ user-friendly interface).
In contrast, most other methods for conjoint analysis require survey administrators to carefully pre-select, or “design”, the questions that are to be asked – with the objective that the resulting “fractional factorial design” is efficient, which usually requires the application of additional methods and software.
Coming up with such an efficient design involves the careful selection of a small subset of alternatives for inclusion in the survey questions from the typically many thousands or millions of combinations of attributes. The resulting number of questions needs to be small enough to not overwhelm decision-makers but still large enough to accurately reveal each attribute’s relative importance.
Fortunately, you don’t need to worry about such design issues with PAPRIKA, and, therefore, as well as being scientifically valid and reliable, PAPRIKA is highly practicable and user-friendly.
Your preferences codified
When you have finished answering PAPRIKA’s trade-off questions, the method uses mathematical techniques (based on linear programming) to calculate your “preference values” or “utilities”, also known as “part-worths”. These values represent the relative importance, or weight, of the criteria and their levels to you (i.e. as revealed by your answers to the trade-off questions).
Examples of preference values and utilities consistent with the earlier examples of prioritizing projects and choosing or designing a car appear in Tables 1 and 2.
Ranked alternatives
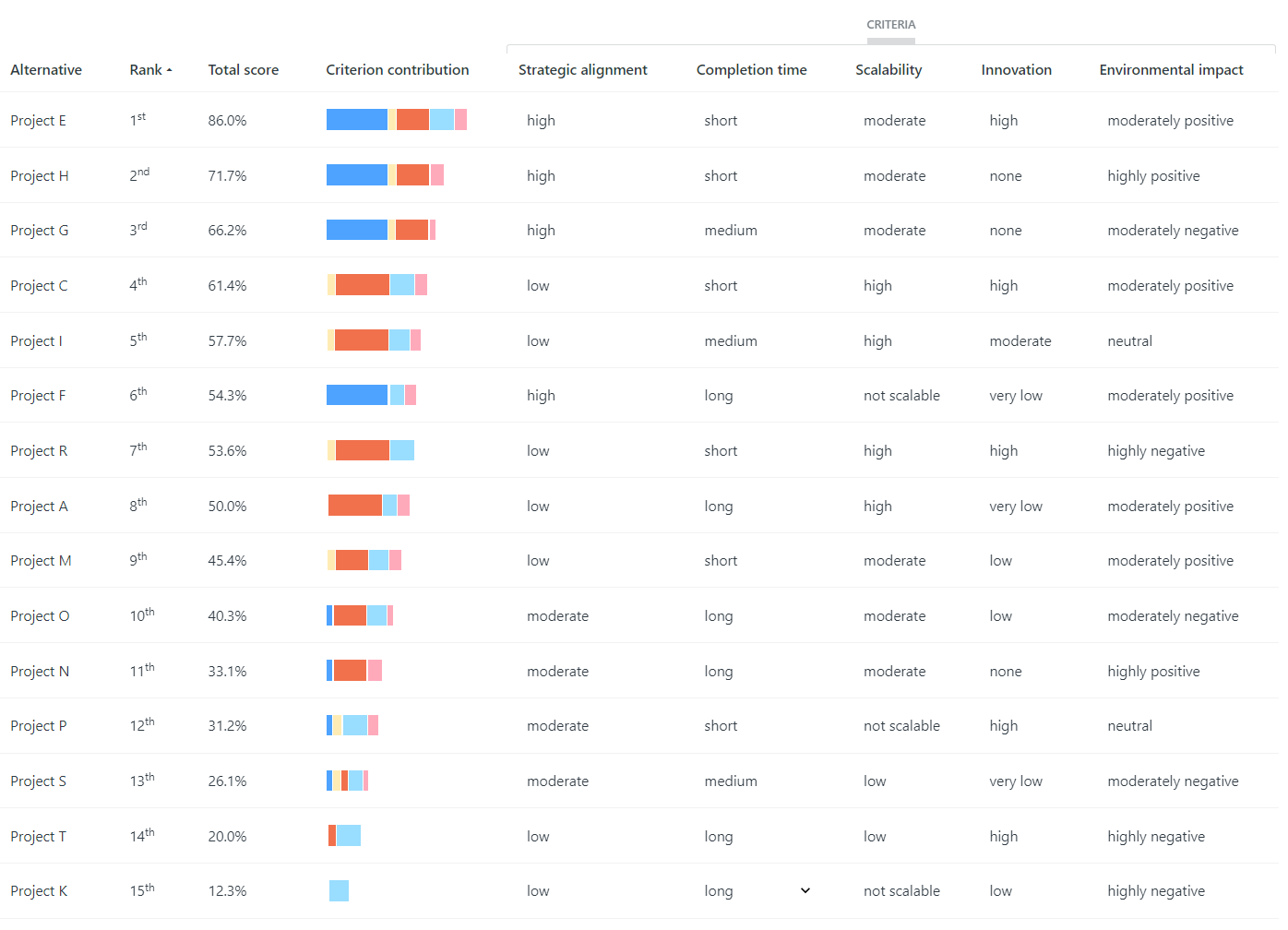
When PAPRIKA has determined your preference values or utilities, 1000minds automatically applies them to produce a ranking of any alternatives you are considering, according to how they are described on the criteria. An illustration for the project-prioritization example appears in Table 3.
1000minds also applies your preference values or utilities to rank all alternatives that are hypothetically possible, i.e. all combinations of the levels on the criteria. This capability is useful when many alternatives are considered over time: e.g. in health and education, 1000s of patients or students may need to be prioritized, such as for health care or scholarships, on an ongoing basis, including in real time.
Validating and applying your results
Before finalizing your results, it’s good practice for you to consider their face validity by thinking about the plausibility of the relative importance of the criteria implied by their preference values or utilities. Do these weights seem about right to you? Are you able to reconcile any incongruities?
Also, if you want to, it’s easy to check the reliability of your answers to PAPRIKA’s questions by re-answering some or all of them. 1000minds’ user-friendliness and PAPRIKA’s adaptivity ensures that any changes to your answers can be easily made and are automatically carried through to your results.
If desired, perhaps later, you can easily revise the criteria and levels without repeating the entire PAPRIKA process. New criteria can be added or obsolete ones deleted without affecting the others. You will only be asked new trade-off questions to determine how the new criteria relate to the existing ones with respect to their relative importance.
When you are happy with your results, 1000minds has tools for interpreting, analyzing and applying them in your decision-making or conjoint analysis application.
Decision-making
Most decision-making applications involve ranking, prioritizing or selecting alternatives. 1000minds has powerful and user-friendly tools for comparing alternatives, including for performing sensitivity analysis with respect to changes in alternatives’ ratings on the criteria and how this affects their ranking.
In addition, some applications, such as investment or project decision-making (e.g. CAPEX), involve the allocation of budgets or other scarce resources across alternatives, typically with the objective of maximizing “value for money” and efficiency. 1000minds includes a powerful resource-allocation framework.
Conjoint analysis
Further analyses of the utilities and rankings of the alternatives you are considering are supported by 1000minds, mostly automatically. As illustrated here, these analyses include:
- attribute rankings
- attribute “relative importance” ratios
- market shares
- “what if” simulations (predictions) based on changes to alternatives’ attributes
- marginal willingness-to-pay (MWTP) estimates from the utilities
An important characteristic of PAPRIKA is that utilities are elicited for each individual participant in a 1000minds conjoint analysis survey instead of being produced at the aggregate level across all participants only (as for most other methods). Such individual-level data is suitable for cluster analysis – e.g. using Excel or a statistics package – to identify “clusters”, or “market segments”, of people with similar preferences.
That ends our introduction to 1000minds’ “secret spice”, the PAPRIKA method. If you haven’t already, you might like to give PAPRIKA a go now!
If you’re still interested (we hope you are!), more detailed information about PAPRIKA is available below.
Want to learn more about PAPRIKA?
The sections below are devoted to answering these questions that will be of interest to many people:
- Why are PAPRIKA’s trade-off questions the easiest for eliciting people’s preferences?
- What limits the number of questions asked so that PAPRIKA is user-friendly?
- How does PAPRIKA compare with other common methods for MCDA and conjoint analysis?
- How is PAPRIKA related to data mining and machine learning?
More technical information about PAPRIKA, including step-by-step demonstrations of the algebra and calculations underpinning the method for a simple example, are available from these peer-reviewed sources:
- A comprehensive overview is available from the Wikipedia article
- For technical information, here is our journal article: P Hansen & F Ombler (2008), “A new method for scoring multi-attribute value models using pairwise rankings of alternatives”, Journal of Multi-Criteria Decision Analysis 15, 87-107
Why are PAPRIKA’s trade-off questions the easiest for eliciting people’s preferences?
PAPRIKA’s questions involve the simplest possible trade-offs for people to think about because they are based on just two criteria or attributes at a time, e.g. see Figures 3 and 4 below. As well as being quick to answer, you can have confidence in your answers.
Simplest possible trade-offs
Indeed, when you think about it … choosing one alternative from two, and when the alternatives are defined on just two criteria at a time, is the easiest question involving a trade-off that you can ever be asked – in all possible universes!
In contrast, choosing one alternative from three or more alternatives is more difficult, as is choosing between alternatives defined on more than two criteria. In general, as the number of alternatives and/or criteria goes up, the cognitive difficulty increases because there are increasingly more trade-offs to keep track of and weigh up in each question.
Clearly, two alternatives and two criteria are the minimum possible (with just one alternative or criterion, there is no trade-off to consider and hence no choice to make). Thus, PAPRIKA’s trade-off questions are the simplest possible.
As mentioned earlier, after answering questions with two criteria at a time, it is possible to go to the “next level of decision-making” by answering questions with three criteria, and then four, etc, up to the number of criteria for your application. However, for most applications, including 1000minds preferences surveys, answering questions with just two criteria is usually sufficient.
Partial vs full profiles
In technical terms, PAPRIKA’s trade-off questions are based on what are known as “partial profiles”: where the two hypothetical alternatives in each question – in conjoint analysis, sometimes called a “choice set” – are defined on just two criteria or attributes at a time (see Figures 3 and 4 again); and where, in effect, the other criteria/attributes for the application are treated as being the same in each question.
In contrast, most other methods are based on more complex and cognitively difficult trade-off questions involving “full profiles”: where the alternatives you are asked to choose between are defined on all criteria for the application together, e.g. six or more criteria – even, in extreme applications, a dozen or more criteria together!
To appreciate the complexity and cognitive difficulty of answering full-profile questions, imagine each pair of hypothetical alternatives you are asked to choose between in Figures 3 and 4 has six or more criteria instead of just two, as with PAPRIKA.
How easy would you find answering such full-profile questions? (Think about all the comparisons you would have to keep track of across the six or more criteria included in each question.) How much confidence would you have in your answers?
The obvious advantage of PAPRIKA’s simple partial-profile questions – just two criteria at a time (Figures 3 and 4) – is that they are easy to think about so that most people can answer them quickly and with confidence in the validity and reliability of their answers.
The superiority of partial-profile questions is confirmed by the common finding in the academic literature that conjoint analysis based on partial profiles more accurately reflects people’s true preferences than full-profile conjoint analysis (Chrzan 2010; Meyerhoff & Oehlmann 2023).
Non-attendance and prominence
Two potentially important sources of bias from full-profile conjoint analysis arising from two heuristics, or mental short-cuts, when people make choices are documented in the literature: (1) the “prominence effect” (Tversky, Sattath & Slovic 1988; Fischer, Carmon, Ariely & Zauberman 1998), and (2) “attribute non-attendance” (Hensher, Rose & Greene 2005).
The prominence effect is the phenomenon whereby when you are asked to choose between full-profile alternatives you select the one with the higher level on the attribute that you think is most important, or “prominent”. In conjoint analysis, the price of the products being compared is a common example of a prominent attribute, especially for consumers who are highly price sensitive.
Similarly, but not the same, attribute non-attendance is when you ignore one or more of the attributes in the full-profiles alternatives you are asked to choose between – not because you don’t care about these “non-attended attributes” but because you do not understand them (or how they are expressed), or find them too difficult to think about, especially when other attributes are more important or easier to think about.
The prominence effect and attribute non-attendance – i.e. resulting in people unduly fixating on some attributes and ignoring others – undermines the validity of their preferences that are revealed, causing biased conjoint analysis results or decision-making outcomes.
Clearly, because PAPRIKA’s partial-profile questions only contain two attributes at a time, they are far less prone to these potential sources of bias.
On the other hand, it’s perhaps tempting to criticize partial profiles – in the extreme, just two attributes in each question (choice set) – as being overly-simplistic representations of real-world decision-making.
Such a criticism is spurious, however, because the fundamental purpose of conjoint analysis and Multi-Criteria Decision Analysis (MCDA) respectively is not to accurately replicate real-world decision-making per se. For conjoint analysis, the purpose is to generate valid and reliable data about what matters to people when they make choices, and for MCDA it is to improve the accuracy (validity and reliability) of decision-making.
Voting and consensus
Another advantage of the simplicity of PAPRIKA’s trade-off questions is that they are especially suited to group decision-making whereby people express their preferences by voting on the answers to the trade-off questions, one question at a time. (As well as a voting option, 1000minds has a suite of survey-based tools for group decision-making involving potentially 1000s of people.)
When there are disagreements in how people voted on a question and the votes are split – which is entirely natural and to be expected (and celebrated!) – with just two criteria to focus on, the opposing viewpoints can be easily discussed in pursuit of consensus. The process of reaching consensus ensures greater face validity.
The following user-friendly voting process is available from 1000minds.
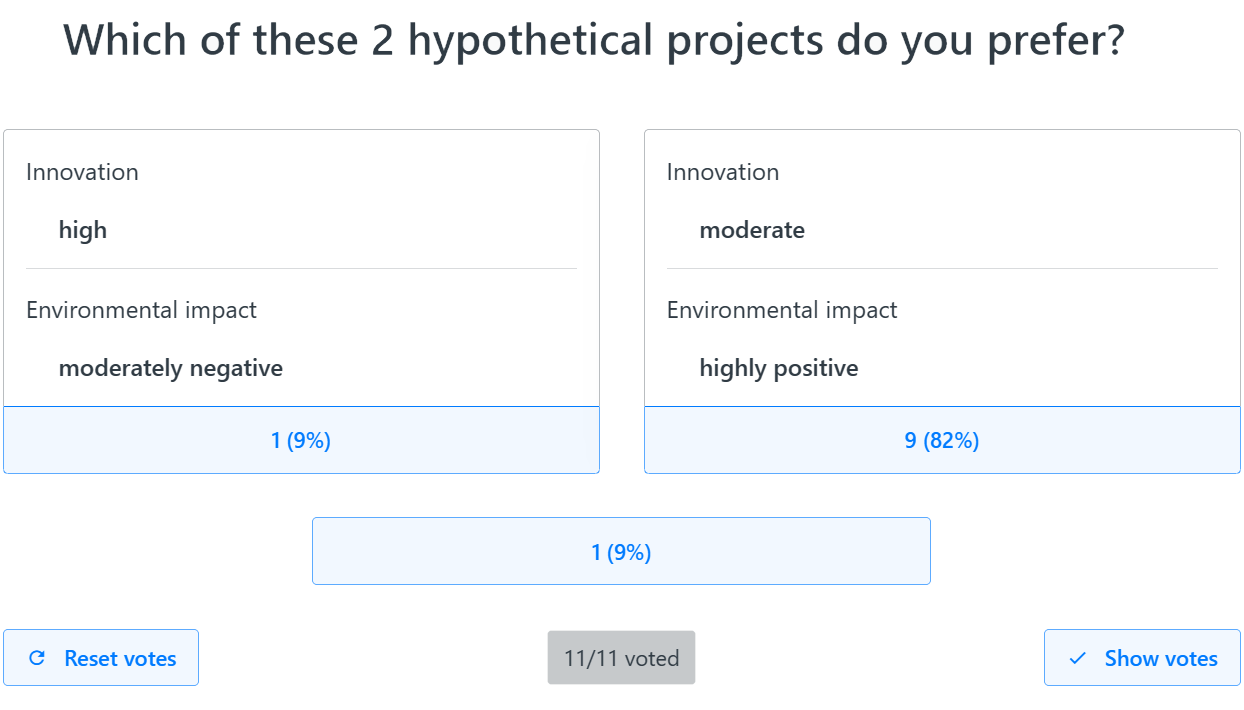
- Participants anonymously vote on each question, one by one, using their mobile devices as clickers (if in the same room) or via online meeting software (if geographically dispersed) connected to 1000minds – by choosing on their screen either the alternative on the left or the right or “they are equal”.
- After each vote, the moderator leading the session clicks the “show votes” button, which reveals on the shared screen how participants voted across the three possible answers; see Figure 5 for an example.
- If there is full agreement (unanimity), the moderator clicks the corresponding choice on the shared screen, and then the next question to be voted on appears on everyone’s screens.
- If the vote is not unanimous, this can be handled in several possible ways, such as: with just one dissenter, they can either accept the majority vote or join in a group discussion in pursuit of consensus; with more dissenters, there can be discussion and consensus and re-voting (“reset votes” in Figure 5). On the rare occasions when consensus cannot be reached or there are too many participants for consensus-building to be practicable, the final decision can be reached via a majority decision.
- This process repeats until all questions have been voted on and potentially discussed by the group.
For most participants, the voting process is engaging and enjoyable overall, as well as being great for team-building.
Ordinal to interval data: turning lead into gold!
When you are answering its trade-off questions, PAPRIKA is getting you to make ordinal, or ranking, judgments – i.e. which hypothetical alternative do you prefer or are they equal?
From your answers to these simplest of questions, PAPRIKA calculates your preference values or utilities to not only rank alternatives but also to score them on an interval scale – e.g. like temperature scales, such as Celsius or Fahrenheit, or time of day (Stevens 1946).
How is this remarkable alchemy – transforming ordinal data into interval data – accomplished?
Based on your ordinal judgments, PAPRIKA is able to generate preference values and scores with interval scale properties because it is arguably the most successful pure application of the theory of conjoint measurement (Luce & Tukey 1964; Debreu 1959).
In fact, your ordinal judgments are conjoint measurements: you are repeatedly comparing combinations of differences between levels on multiple criteria, and the more such conjoint measurements you perform, the less “wiggle room” there is in the universe of possible preference values consistent with your preferences (your measurements).
In general, the more trade-offs you make, the more certain you can be that the resulting preference values and scores of alternatives reflect your preferences. To understand this further, pay attention to the accuracy indicator and the “possible range” of scores reported inside 1000minds.
If desired, you can even turn gold into platinum with 1000minds’ scaling tools – allowing you to score alternatives on a ratio scale, e.g. to be able to say one alternative is, say, 3-times better than another. This capability is especially important when combining scores with other measures like cost in value-for-money analysis.
What limits the number of questions asked so that PAPRIKA is user-friendly?
Each time you answer a trade-off question – i.e. choose between two hypothetical alternatives, such as “projects” or “cars”, as in Figures 3 and 4 above – PAPRIKA immediately identifies and eliminates from further consideration all other pairs of hypothetical alternatives whose ranking are logically implied by your current answer and all your earlier answers.
These eliminated pairs of hypothetical alternatives correspond to possible trade-off questions that you could be asked but because PAPRIKA knows how they are answered because of your earlier answers, they can be dispensed with so you are not burdened by unnecessary questions.
These eliminated questions are identified by PAPRIKA’s exploitation of the mathematical and hence logical properties of additive “multi-criteria value models” that the method is based on, as explained in the next section.
As well as eliminating questions that you would otherwise unnecessarily be asked, each time you answer a question, PAPRIKA carefully selects the next question to ask you. PAPRIKA’s selection is on the basis that the question it chooses is likely, when you answer it, to eliminate the most possible questions in the future as the process continues. The objective is to minimize the number of questions you are asked so that the method is as practicable and user-friendly as possible.
Again, based on your answer to that next question, all other possible questions that are logically implied by your current answer and all your earlier answers are identified and eliminated, and another question is carefully selected for you to answer next.
This process for identifying possible questions for elimination and new questions for you to answer is repeated until all possible trade-off questions have been either eliminated (the vast majority) or answered by you (a tiny minority).
Properties of additive multi-criteria value models
As referred to above, the possible questions you could be asked but that are eliminated as you answer PAPRIKA’s questions are identified by the method’s clever exploitation on a very large scale of the properties of additive “multi-criteria value models”.
(As explained in an earlier section of this article, like most methods for decision-making and conjoint analysis, PAPRIKA is based on what are known in the academic literature as additive “multi-criteria value models” or “multi-attribute value models” – also commonly referred to as “weighted-sum”, “additive”, “linear”, “scoring”, “point-count” or “points” models or systems.)
Broadly speaking, these properties go by the names of “transitivity”, “monotonicity”, “joint-factor independence” and “double cancellation” (Krantz 1972). Explaining how they are operationalized in 1000minds is outside the scope of this article; for details, see Hansen & Ombler (2008).
Transitivity is easily illustrated via this simplest of possible examples, intended to give you a sense of how this property works and its implications:
- Imagine that you are asked to rank alternative
Xrelative to alternativeY(where these two alternatives are defined on two criteria like the trade-off questions in Figures 3 and 4 above). Suppose you chooseX. - Next, or sometime later, you are also asked to rank
Yversus a third alternative,Z. You chooseY. - Therefore, given you ranked
Xahead ofYandYahead ofZ, then logically – by transitivity! –Xmust be ranked ahead ofZ.
And so PAPRIKA would implicitly rank this third pair of alternatives (X versus Z) and eliminate the corresponding question. Because PAPRIKA already knows the answer to this question thanks to your two earlier answers, you will not be unnecessarily asked it.
A powerful adaptive algorithm
The example above is extremely simple relative to PAPRIKA applications, which typically involve very large numbers of possible questions and hypothetical alternatives. PAPRIKA applies transitivity (as well as the other properties of additive “multi-criteria value models” mentioned above) across many dimensions simultaneously on a very large scale while optimizing the sequence of questions the decision-maker is asked.
This large-scale multi-dimensionality dramatically increases PAPRIKA’s computational complexity. Moreover, the computations must be performed in real time as the questions are answered one by one without making decision-makers wait between questions.
Thus, each time you answer a trade-off question, 1000minds pauses for a split second to “think” about two important issues:
- Which of the other possible questions to eliminate (because their answers are implied by your answers to earlier questions)?
- Which of the remaining questions is the best to ask you next?
PAPRIKA continually adapts as you answer the trade-off questions to ensure that the number of questions is minimized. And yet by answering a relatively small number of questions you end up having pairwise ranked all hypothetical alternatives differentiated on two criteria at a time, either explicitly or implicitly.
PAPRIKA guarantees that your pairwise rankings – answers to the trade-off questions – are consistent, and thus a complete overall ranking of all hypothetically possible alternatives representable by the criteria is determined, based on your preferences.
Finally, your preferences are accurately codified as the preference values or utilities generated by PAPRIKA, which are used to rank any alternatives you are considering.
Eureka!
The PAPRIKA method, as implemented in 1000minds, achieves the remarkable feat – hence, the patents and awards – of keeping track of all the potentially millions of pairwise rankings of all hypothetically possible alternatives implied by each decision-maker’s answers to the trade-off questions.
In other words, PAPRIKA identifies Potentially All Pairwise RanKings of all possible Alternatives representable by the criteria for your application; hence, the acronym for the method’s full name: PAPRIKA.
PAPRIKA keeps track of all these pairwise rankings efficiently and in real time, ensuring the number of questions you are asked is minimized so that the method is as practicable and user-friendly as possible.
Technical details are available in Hansen and Ombler (2008), including a step-by-step demonstration of the algebra and calculations underpinning PAPRIKA for a simple example involving three criteria with two levels each.
How many questions and how long do they take?
The number of trade-off questions you are asked depends on how many criteria and levels you specified for your application: the more criteria and/or levels, the more questions.
For most applications, fewer than a dozen criteria is usually sufficient, though more are possible and 4 to 8 is fairly typical.
With respect to the criteria’s levels, there is usually no requirement that the criteria have the same number of levels each, e.g. some can have three levels, others four, five, etc – whatever is appropriate for your application.
If you had, for example, four criteria and three or four levels each, you would be asked approximately 25 questions; with six criteria, ~42 questions; with eight criteria, ~60 questions, etc.
Because PAPRIKA’s questions are the easiest possible involving trade-offs, they are quick to answer. For example, most participants in 1000minds preferences surveys can comfortably answer 4 to 6 questions per minute.
And so for the three examples above:
- 4 criteria and 3 or 4 levels each: ~25 questions, taking less than 10 minutes for most people
- 6 criteria and 3 or 4 levels each: ~42 questions, taking less than 15 minutes
- 8 criteria and 3 or 4 levels each: ~60 questions, taking less than 20 minutes
Thus, in addition to being scientifically valid and reliable, PAPRIKA is highly practicable and user-friendly.
It’s also worthwhile noting that, for obvious reasons, the time required to answer PAPRIKA’s questions depends on the length and intricacy of the language used for the criteria and levels: the shorter and simpler, the better. Decision-makers’ expertise and how engaged they are also matters, as well as the application’s overall complexity.
Also, it typically takes longer if you use 1000minds’ voting option for groups to answer the questions by voting on them one question at a time and discuss disagreements in pursuit of consensus. On the other hand, it is usually a highly productive and enjoyable team-building exercise!
Path dependence
The numbers of trade-off questions asked by PAPRIKA reported above for the three examples of applications with four, six and eight criteria respectively were approximate estimates instead of being precise statistics: ~25, ~42 and ~60 questions respectively.
This imprecision is because the number of questions you are asked depends on how you answer them. And so, because of PAPRIKA’s adaptivity, the questions exhibit “path dependence” – which, in the present context, means that if you were to answer the questions differently, you would be asked different questions, typically resulting in different numbers of questions each time.
Likewise, when groups of people are individually faced with the same set of possible questions, as for a 1000minds preferences survey, because people’s preferences are likely to be idiosyncratic, they will answer at least some of their questions differently. Hence, they are likely to answer different numbers of questions each.
This phenomenon of path dependence is easily illustrated by returning to the earlier simple example used to illustrate the logical property of transitivity and asking a second person the same questions asked of the first person in the earlier example:
- Imagine that the second person answers the first question,
XversusY, the same as the first person:Xahead ofY. - But they answer the second question,
YversusZ, the opposite to the first person’s ranking:Zahead ofY. - This time, given that this second person ranked
Xahead ofYandZahead ofY, we know nothing about how they would rankXversusZ. Therefore, they would need to be asked this third question.
Thus, in this second example, the second person would be asked all three trade-off questions instead of just the two asked of the first person in the first example.
To help you when thinking about how many criteria and levels to specify for your application, 1000minds has a useful simulation tool for estimating how many questions will be asked.
An example of the simulation results based on six criteria and three or four levels each appears in Figure 6: thus, you could expect to be asked 42 questions on average, based on 14 simulations ranging from a minimum of 30 questions to a maximum of 60.
Given most people can comfortably answer 4 to 6 questions per minute, most people should be able to answer these 30 to 60 questions in under 15 minutes.

How does PAPRIKA compare with other common methods for MCDA and conjoint analysis?
Decision-making and conjoint analysis are large fields in academia, business, nonprofits and government, with long and illustrious histories. Unsurprisingly, therefore, in addition to PAPRIKA, other methods are available for determining people’s preference values or utilities (representing the relative importance of the criteria/attributes in the application).
The two most widely used of these other methods are:
- Analytic Hierarchy Process – for Multi-Criteria Decision Analysis (MCDA)
- Logistic regression analysis – mostly for conjoint analysis
These two methods are discussed in turn below in comparison to the PAPRIKA method (so that you can have confidence in choosing PAPRIKA!).
How does PAPRIKA compare with the Analytic Hierarchy Process (AHP)?
From a user’s perspective, PAPRIKA’s defining characteristic is that it is based on pairwise (ordinal) rankings of alternatives – e.g. see Figures 7 and 8 below.
In contrast, as invented by Thomas Saaty (Saaty 1977, 1980), the Analytic Hierarchy Process (AHP) involves decision-makers expressing how they feel about the relative importance of the criteria on a ratio scale, known as ratio-scale measurements.
Here is a generic example of an AHP ratio-scale question:
On a nine-point scale ranging from “equally preferred” (ratio = 1) to “extreme importance” (ratio = 9), how much more important is criterion A than criterion B?
Such a question corresponding to the project-prioritization criteria in Figure 7 below would be:
On a nine-point scale ranging from “equally preferred” (ratio = 1) to “extreme importance” (ratio = 9), when thinking about prioritizing projects, how much more important is “strategic alignment” than “innovation potential”?
Similar ratio-scale questions are used to elicit how people feel about the performance of any alternatives under consideration on each criterion in turn, such as:
On a nine-point scale ranging from “equally preferred” (ratio = 1) to “extremely preferred” (ratio = 9), with respect to “strategic alignment”, how more do you prefer Project X to Project Y”?
AHP’s cognitively difficult questions
The obvious weakness of AHP is that most people find answering its ratio-scale questions cognitively difficult. (How easy would you find answering the AHP examples above?)
Thinking about how strongly you feel about one criterion, or alternative, relative to another and expressing that strength of preference on a ratio scale, even with verbal equivalents, is an unnatural type of mental activity that most people have very little experience of in their lives.
Therefore, it’s easy to question AHP’s validity and reliability – in short, “garbage in, garbage out”.
In contrast, most people find it easy to answer PAPRIKA’s trade-off questions (e.g. perhaps look at Figures 7 and 8 again) – albeit answering such questions involves confronting trade-offs between the criteria, which requires mental effort, of course.
PAPRIKA’ advantage is that pairwise ranking – choosing one alternative from two – is the easiest choice possible. Such choices are a natural type of mental activity that we all engage in dozens if not hundreds of times every day: e.g. “would you like scrambled or poached eggs for breakfast?”, “shall we go out to a movie or stay in and watch Netflix?”, etc.
In the words of Drummond et al. (2015):
The advantage of choice-based methods is that choosing, unlike scaling, is a natural human task at which we all have considerable experience, and furthermore it is observable and verifiable.
In conclusion, PAPRIKA involves simple ordinal or ranking measurements of decision-makers’ preferences, which are easier and more natural than AHP’s more challenging ratio-scale measurements. Therefore, you can have more confidence in your answers to PAPRIKA’s questions, and hence in decisions reached with the help of 1000minds.
How does PAPRIKA compare with logistic regression analysis?
The other popular method to be compared against PAPRIKA goes by the name of “logistic regression analysis” (LRA), which refers to the range of statistical techniques available for processing people’s preferences data as revealed by their choices into preference values or utilities.
Though LRA is available for MCDA, it is mostly used for conjoint analysis for processing participants’ choices – typically, their rankings of hypothetical alternatives – into utilities.
Given LRA encompasses a range of statistical techniques, there are two main dimensions to consider when reviewing LRA: (1) the statistical techniques for processing people’s preferences data, and (2) the methods by which the data was elicited in the first place.
Both dimensions are potentially very large fields for study. As this article is not intended to be as comprehensive as a textbook, the next three sections consist of a short overview of LRA’s statistical techniques, a discussion of the advantages of PAPRIKA’s individual-level data, and, finally, a short review of “design issues” associated with conjoint analysis surveys.
LRA’s statistical techniques
LRA is based on the statistical estimation of what are known as “logistic” or “logit” models. Such models are widely used for predictive modelling for a broad range of applications beyond conjoint analysis, e.g. weather forecasting and economic modelling.
Logistic (logit) models used for conjoint analysis come in a variety of forms, including “nested” and “cross-nested” logits, “probit” and “mixed logit” and hierarchical Bayesian estimation (Train 2009).
These models and the statistical techniques for estimating them are relatively complicated. Most people do not need to be fully abreast of them because they are handled by the specialized software and/or statisticians supporting LRA. Details about LRA models and statistical methods are available in Train (2009).
LRA models can be summarized as modelling the probability of each alternative in a conjoint analysis survey being chosen by participants relative to the other alternatives that could have been chosen instead. The model’s parameters, from which utilities are calculated, are mostly estimated via statistical techniques known as “maximum likelihood methods”: i.e. where the “likelihood function” is maximized such that, consistent with the model’s assumptions, the observed choices are most likely.
Like LRA, PAPRIKA involves sophisticated quantitative methods for calculating the preference values or utilities from each person’s answers to their trade-off questions. However, instead of statistical techniques, PAPRIKA uses linear programming: i.e. where the linear program to obtain the utilities is a system of equalities or inequalities corresponding to the person’s answers. Technical details are available in Hansen and Ombler (2008).
An important practical advantage of PAPRIKA is that the utilities and other conjoint analysis outputs are automatically generated and in real time. In contrast, LRA typically needs more time for processing and often requires expert support from statisticians.
PAPRIKA’s individual-level data
Another important and advantageous characteristic of PAPRIKA is that the utilities (representing people’s preferences) are elicited for each individual participant in a conjoint analysis survey – in contrast to most other methods which produce aggregate results only from the group of participants surveyed. As explained later below, individual-level data enables the heterogeneity of people’s preferences to be modelled and used for predicting how individuals and particular sub-groups will behave.
An LRA technique that also results in the generation of individual utilities for each survey participant but by incorporating information from across all participants is hierarchical Bayesian (HB) estimation (Allenby, Arora & Ginter 1995).
The HB algorithm begins by estimating each participant’s utilities based on their choices expressed in the survey and also the mean utilities for the sample overall. And then, typically over many thousands of iterations, these estimates are adjusted (or “updated”) by applying a statistical model based on all participants and taking into account their heterogeneity along with assumptions about their utilities’ distribution.
In contrast to HB estimation, PAPRIKA determines each participant’s utilities directly for that individual, independently of others in the sample. Also, PAPRIKA is arguably easier to understand with respect to its underlying mathematical concepts and because PAPRIKA operates in real time it is faster than HB’s iterative approach.
PAPRIKA’s individual-level data can be used for cluster analysis – e.g. performed using Excel or a statistics package such as SPSS or MATLAB – to identify “clusters”, or “market segments”, of participants with similar preferences as captured by their utilities.
Subsequent analysis – e.g. multinomial logit regression analysis – can investigate if participants’ likelihoods of belonging to a particular cluster or market segment are related to their socio-demographic and background characteristic (also collectible in 1000minds surveys). Such information is useful, for example, for marketing campaigns for business applications or government policy-making.
Market simulations, or the posing of “what if” questions, can also be conducted using PAPRIKA’s individual-level data. Changes to an alternative’s attributes can be traced through to predict how each participant in a conjoint analysis survey would be expected to respond with respect to their choices and the corresponding effect on the alternatives’ “market shares”.
Conjoint analysis design issues
As mentioned earlier, LRA (i.e. logistic regression analysis) is used mostly for conjoint analysis rather than for decision-making. Except for PAPRIKA, most conjoint-analysis methods require the careful pre-selection, or “design”, of the questions (or “choice sets”) to be asked in the conjoint analysis survey, with the objective that the resulting “fractional factorial design” is efficient.
Coming up with an efficient “fractional factorial design” – usually requiring specialized methods and software – entails specifying the questions based on a tiny subset of alternatives (or “profiles”) from the full set representable by all possible combinations of the attributes (potentially numbering in the many thousands or millions). The resulting number of questions should be small enough to be practicable to be asked in the survey but still large enough to assess each attribute’s relative importance.
For a design to be efficient it usually also needs to be balanced and orthogonal. “Balanced” means that each level in each attribute appears in the questions the same number of times, and “orthogonal” means that if a pair of levels are selected from one attribute and another, the pairs appear the same number of times in the design. (Incidentally, a symmetrical design is where the attributes have the same number of levels each; an asymmetrical design does not.)
You don’t need to worry about such design issues with PAPRIKA. People’s preferences are elicited adaptively and interactively – and automatically – by the method asking the minimum number of trade-off questions required to pairwise rank all hypothetical alternatives defined on two attributes at a time, either explicitly or implicitly.
This result is the source of PAPRIKA’s name, being an acronym for the method’s full name: Potentially All Pairwise RanKings of all possible Alternatives – i.e. the PAPRIKA method results in “potentially all pairwise rankings of all possible alternatives” being identified.
As well as being user-friendly for survey participants, conjoint analysis surveys based on PAPRIKA are very easy for administrators to set up.
See also
Wikipedia article about PAPRIKA method
References
K Chrzan (2010), “Using partial profile choice experiments to handle large numbers of attributes”, International Journal of Market Research 52, 827-40
G Debreu (1959), “Topological methods in cardinal utility theory”, Cowles Foundation Discussion Papers, 76
M Drummond, M Sculpher, G Torrance, B O’Brien & G Stoddart (2015), Methods for the Economic Evaluation of Health Care Programmes, Oxford University Press
G Fischer, Z Carmon, D Ariely & G Zauberman (1998), “Goal-based construction of preferences: task goals and the prominence effect”, Management Science 45, 1057-75
P Hansen & F Ombler (2008), “A new method for scoring multi-attribute value models using pairwise rankings of alternatives”, Journal of Multi-Criteria Decision Analysis 15, 87-107
R Hastie & R Dawes (2010), Rational Choice in an Uncertain World. The Psychology of Judgment and Decision Making, Sage Publications
D Hensher, J Rose & W Greene (2005), “The implications on willingness to pay of respondents ignoring specific attributes”, Transportation 32, 203-22
D Kahneman (2011), Thinking, Fast and Slow, Farrar, Straus and Giroux
D Kahneman, O Sibony & O Sunstein (2021), Noise: A Flaw in Human Judgment , Little, Brown Spark
D Krantz (1972), “Measurement structures and psychological laws”, Science 175, 1427-35
R Luce & J Tukey (1964), “Simultaneous conjoint measurement: A new type of fundamental measurement”, Journal of Mathematical Psychology 1, 1-27
J Meyerhoff & M Oehlmann (2023), “The performance of full versus partial profile choice set designs in environmental valuation”, Ecological Economics 204, 107665
T Saaty (1977), “A scaling method for priorities in hierarchical structures”, Journal of Mathematical Psychology 15, 234-81
T Saaty (1980), The Analytic Hierarchy Process: Planning, Priority Setting, Resource Allocation”, McGraw-Hill
S Stevens (1946), “On the theory of scales of measurement”, Science 103, 677-80
K Train (2009), Discrete Choice Methods with Simulation, Cambridge University Press
A Tversky, S Sattath & P Slovic (1988), “Contingent weighting in judgment and choice”, Psychological Review 95, 371-84