Pairwise comparison method

Pairwise comparisons, and pairwise rankings in particular, are central to many methods for performing Multi-Criteria Decision Analysis, including 1000minds.
This is the ultimate guide to understanding pairwise comparisons and pairwise rankings, and is an essential resource for practitioners and academics alike. Whatever your level of background knowledge, this article is for you!
A similarly comprehensive article on Multi-Criteria Decision Analysis (MCDA), also known as Multi-Criteria Decision-Making (MCDM), is also available.
What is pairwise comparison?
The pairwise comparison method (sometimes called the paired comparison method) is a process for ranking or choosing from a group of alternatives by comparing them against each other in pairs, i.e. two alternatives at a time. Pairwise comparisons are widely used for decision-making, voting and studying people’s preferences.
How does the pairwise comparison method work?
The pairwise comparison method works by each alternative being compared against every other alternative in pairs – i.e. “head-to-head”. The decision-maker pairwise ranks the alternatives in each pair: by deciding which one is higher ranked or if they are equally ranked.
Typically, all possible pairs of alternatives are pairwise compared and pairwise ranked against
each other. For n alternatives, there are n(n−1)/2
possible pairwise comparisons and rankings; e.g, with 5 alternatives, there are 10 pairwise
comparisons, resulting in 10 pairwise rankings.
What is pairwise ranking?
Pairwise ranking is the process of pairwise comparing alternatives and ranking them by choosing the alternative in the pair that is higher ranked (e.g. preferred) or choosing them both if they are equally ranked (e.g. indifference).
This process is repeated with different pairs of alternatives, typically until all possible pairs have been pairwise ranked. The pairwise rankings are usually combined to produce an overall ranking of the alternatives or to identify the top-ranked or preferred (“best”) one.
As an example, suppose you want to take your family on vacation. There are many great destinations around the world, and so to make your decision easier you can pairwise compare and rank each destination against all other possibilities. For example, you might prefer Disney World over San Francisco, and Cancún over Disney World, and so on for all other possible pairs of destinations you are considering. Through a series of such pairwise rankings, perhaps you find Cancún to be the best vacation spot for you.
Pairwise ranking is useful because it simplifies and improves the accuracy of your decision-making. Pairwise ranking’s potency derives from the fundamental principle that an overall ranking of alternatives is defined when all pairwise rankings are known – provided the pairwise rankings are consistent with each other (which, as discussed below, depending on the scale of the application and the sophistication of the method used, is often not the case).
To help you appreciate this relationship between pairwise and overall rankings, as an illustration, suppose you wanted to rank everyone in a group of people from the youngest to the oldest (or from the shortest to the tallest, etc). If you knew how each person was pairwise ranked relative to everyone else – i.e. for each possible pair of individuals, you identified the younger person or that they are the same age – then you could produce an overall ranking from the youngest to the oldest.
Pairwise ranking and voting theory
In the example above and the remainder of this article, the pairwise rankings are performed by an individual decision-maker. In most cases, this individual decision-maker will be a single person, but could also be a group of people working together (e.g. by consensus) as a single decision-making entity.
Other pairwise ranking applications involve multiple individual decision-makers, each making potentially different decisions. A classic example is voters choosing a leader from a list of candidates in an election or ranking preferred policies (e.g. national pension schemes) in a referendum. Equivalent examples from outside public politics include electing board members, etc.
In such applications involving multiple decision-makers (voters), it is necessary for each voter’s pairwise rankings (and their consequent overall ranking) to be aggregated across a potentially very large number of voters, including resolving the almost inevitable conflicts in their rankings. Methods for performing such aggregations are known in the social choice literature as social choice functions or voting rules.
Examples include the Condorcet Method and the Borda, Copeland and Simpson Rules
(and other methods/rules too). These methods were devised by the 18th century French political
philosophers, the Marquis de Condorcet (
Pairwise comparison methods and tools
For an individual decision-maker (single person or group working together) to perform pairwise comparisons for relatively small-scale applications involving at most just a handful of alternatives, a simple pairwise comparison chart can be used. Other manual though slightly more sophisticated methods are also available, such as Benjamin Franklin’s “moral or prudential algebra” or the even-swap method. These three manual methods are explained in turn below.
However, a weakness of these relatively simple manual methods is that they do not scale-up well for applications involving more than just a handful of alternatives. Therefore, as explained later, for larger-scale or higher-stake applications involving more alternatives and multiple criteria for choosing between them, specialized decision-making software based on more sophisticated algorithms such as 1000minds’ PAPRIKA method, are available.
Pairwise comparison charts
A simple way to implement the pairwise comparison method is to use a pairwise comparison chart (sometimes called a paired comparison chart). As an illustration, imagine you want to hire someone for a job from a short-list of five candidates, who you want to rank from first to fifth, i.e. best to worst.
Start by creating a pairwise comparison table, as in Table 1 below, with the candidates listed down the left hand-side and also along the top. Or download our free workbook (Tables 1-5 below) to follow along!
| Neha | Peter | Sajid | Bao | Susan | |
|---|---|---|---|---|---|
| Neha | – | ||||
| Peter | – | ||||
| Sajid | – | ||||
| Bao | – | ||||
| Susan | – |
Next, pairwise compare each candidate in a row to a different candidate in a column and pairwise rank them according to who you prefer. Keep track using the following simple scoring system.
If you prefer the row candidate over the column candidate (e.g. Neha vs Peter), enter 1 in that cell, and enter 0 in the inverse cell (Peter vs Neha), as in Table 2. Notice that the pairwise comparisons on either side of table’s central diagonal (i.e. a person compared to themselves – marked with dashes), are inverses of each other.
Alternatively, if you think the column candidate is better than the row candidate, enter 0, and enter 1 in the inverse cell. If both candidates are equally good, enter 0.5 in both cells.
| Neha | Peter | Sajid | Bao | Susan | |
|---|---|---|---|---|---|
| Neha | – | 1 | 1 | 0 | 0.5 |
| Peter | 0 | – | 0 | 1 | 0 |
| Sajid | 0 | 1 | – | 1 | 0 |
| Bao | 1 | 0 | 0 | – | 0 |
| Susan | 0.5 | 1 | 1 | 1 | – |
After having completed all 10 pairwise comparisons, for each candidate add up their points across the row to get their total scores:
- Neha:
1 + 1 + 0 + 0.5 = 2.5 - Peter:
0 + 0 + 1 + 0 = 1 - Sajid:
0 + 1 + 1 + 0 = 2 - Bao:
1 + 0 + 0 + 0 = 1 - Susan:
0.5 + 1 + 1 + 1 = 3.5
Use the candidates’ total scores to rank them. We can see that Susan, with 3.5 points, is in 1st place, followed by Neha (2nd), Sajid (3rd), and Peter and Bao are tied for 4th equal.
Practical drawbacks of pairwise comparing alternatives holistically
Using a pairwise comparison chart is straight-forward when there are only a few alternatives, as in the example above. But how would you manage if there were, say, 20, 200 or even 2000 alternatives to be pairwise ranked?
With n alternatives, there are n(n−1)/2 pairwise
rankings (not counting inverses). In the example above with 5 alternatives, there were 10
pairwise rankings (i.e. 5(5-1)/2 = 10). With 20, 200 or 2000 alternatives, there
would be 190, 19,900 or 1,999,000 pairwise rankings. A lot!
Clearly, the practicality of using a pairwise comparisons chart decreases dramatically as the number of alternatives increases.
Aside from the sheer volume involved, pairwise comparisons based on holistic assessments of the alternatives – involving mentally working through all the possible reasons for favoring one alternative over another – tends to be cognitively difficult. There is a lot to think about and keep track of. Hence, you are very likely to make mistakes, which could have serious implications for the accuracy of the overall ranking or the top-ranked alternative identified.
Transitivity
One common error that is especially worthwhile discussing is violation of an important logical property of so-called rational or consistent decision-making known as transitivity. Transitivity is easily explained as follows.
Suppose that when you are asked to pairwise rank two alternatives, A
versus B, you rank A over B. And then you also pairwise
rank B over a third alternative, C. These two pairwise rankings imply
that, logically – by transitivity! – you should also rank A over C
(i.e. if A > B and
B > C then A > C).
Imagine, instead, that when you are asked to pairwise rank A versus C,
you rank C over A. Then you are violating transitivity.
This final pairwise ranking (C > A) would be inconsistent,
wouldn’t it? Arguably, such decision-making is irrational.
Such inconsistency has serious implications for your ability to settle on an overall ranking of the three alternatives, A, B and C. If you are intransitive as above, you will go round in circles successively pairwise ranking the alternatives.
For example, if, as above, you rank C over A and also A over B, what does that imply for C versus B? It implies C is ranked over B. But that is in contradiction of the second pairwise ranking above, B over C. And so on: round and round you go!
Are the pairwise rankings in the hiring example above consistent (transitive)?
From Table 2 above, it can be seen that Neha is preferred to Peter, and Peter is preferred to Bao. These two pairwise rankings imply Neha is preferred to Bao – and yet we can see that Bao is recorded as preferred to Neha. This inconsistency highlights a risk that the overall ranking of the five short-listed candidates arrived at earlier, including that Susan is the best candidate, is unreliable.
There are no guarantees of consistency when pairwise ranking is performed manually (or, indeed, when some software tools are used!).
On the other hand, transitivity is automatically applied by 1000minds software’s “pairwise sorting” tool, whereby you can sort a list of alternatives – up to a maximum of 30 – by pairwise ranking them holistically (1000minds also implements the PAPRIKA method for Multi-Criteria Decision Analysis explained later below).
Here are two examples:
By ensuring transitivity, 1000minds significantly reduces the number of pairwise rankings
you need to perform. Without the tool, to rank 10 and 16 alternatives respectively would
require 45 and 120 pairwise rankings (applying the n(n−1)/2 formula above,
and assuming the rankings are all consistent). But with the tool just 19 and 35 pairwise
rankings respectively are required on average.
Explicit criteria for ranking or choosing between alternatives
A common solution to the practical drawbacks of pairwise ranking alternatives holistically, especially when you have more than just a few alternatives to consider is to formulate the decision problem in terms of explicit criteria (or “objectives”) for ranking or choosing between the alternatives.
In the hiring example above, these criteria might be the candidates’ education, experience, social skills, references, etc. Or imagine you were choosing a car to buy: your criteria would probably include things like fuel efficiency, safety, engine power, styling, price, etc.
The remainder of this article is devoted to five pairwise comparison methods based on the application of explicit criteria to rank or choose between alternatives.
These methods are from the field of Multi-Criteria Decision Analysis (MCDA), also known
as Multi-Criteria Decision-Making (MCDM). A sub-discipline of operations research with
foundations in economics, psychology and mathematics
(
A comprehensive overview of MCDA / MCDM, which, like the present article, is intended as an essential resource for practitioners and academics (including students), is available here.
MCDA / MCDM methods are often based on pairwise comparisons, involving either the implicit or explicit weighting of criteria, representing their relative importance for the decision at hand.
The first two pairwise comparison methods below are based on the implicit weighting of criteria, and were designed to be performed manually (before the advent or widespread availability of computers).
The last three methods below – the Analytic Hierarchy Process (AHP), conjoint analysis or discrete choice experiments (DCE) and 1000minds’ PAPRIKA method – involve explicit weighting and are implemented using specialized software. These methods were created for larger-scale or higher-stake decisions involving potentially many alternatives.
Benjamin Franklin’s “moral or prudential algebra”
Historically, the first example of an MCDA method based on pairwise comparisons was described
by Benjamin Franklin in 1772 (
As Franklin explains, this method involves listing the “pros” and “cons” of the alternative being considered relative to another alternative (e.g. the status quo) and then successively trading-off the pros and cons. These trade-offs are based on implicitly weighting the pros and cons (equivalent to criteria or objectives) according to their relative importance in a series of pairwise comparisons, resulting in the preferred alternative being identified.
London
Sept. 19, 1772Dear Sir,
In the affair of so much importance to you, wherein you ask my advice, I cannot, for want of sufficient premises, advise you what to determine, but if you please I will tell you how.
When those difficult cases occur, they are difficult, chiefly because while we have them under consideration, all the reasons pro and con are not present to the mind at the same time; but sometimes one set present themselves, and at other times another, the first being out of sight. Hence the various purposes or inclinations alternatively prevail, and the uncertainty that perplexes us.
To get over this, my way is to divide half a sheet of paper by a line into two columns; writing over the one Pro, and over the other Con. Then, during three or four days consideration, I put down under the different heads short hints of the different motives, that at different times occur to me, for or against the measure.
When I have thus got them all together in one view, I endeavor to estimate their respective weights; and where I find two, one on each side, that seem equal, I strike them both out. If I find a reason pro equal to two reasons con, I strike out the three. If I judge some two reasons con, equal to some three reasons pro, I strike out the five; and thus proceeding I find at length where the balance lies; and if, after a day or two of further consideration, nothing new that is of importance occurs on either side, I come to a determination accordingly.
And, though the weight of reasons cannot be taken with the precision of algebraic quantities, yet, when each is thus considered, separately and comparatively, and the whole lies before me, I think I can judge better, and am less liable to make a rash step; and in fact I have found great advantage from this kind of equation, in what may be called moral or prudential algebra.
Wishing sincerely that you may determine for the best, I am ever, my dear friend, yours most affectionately,
B. Franklin
For small-scale applications with just two alternatives, Franklin’s approach is as potent today as it was back in his day. But when there are extra alternatives to consider, more sophisticated and scalable methods are required.
Even-swap method
The even-swap method (
As an illustration, suppose you own a business that is expanding and you want to choose a new workplace with more space from a short-list of five addresses.
Start by creating a consequences table (sometimes called a performance matrix), as in Table 3 below. The five alternatives (addresses) are listed down the left hand-side and the criteria for choosing between them are across the top (for now, ignore the strikethroughs in the table). Or download our free workbook (Tables 1-5) here to follow along!
| Address | Floor space (m2) | Quality of work facilities | Quality of local amenities | Quality of public transport | Monthly rent ($) |
|---|---|---|---|---|---|
| 6 Yellow Brick Road | 400 | medium | medium | medium | 5000 |
| 23 Happy Valley | 400 | high | low | high | 6000 |
| 77 Sunshine Lane | 550 | low | medium | high | 7500 |
Next, with the objective of reducing the number of alternatives you have to deal with as you attempt to zero in on the best one, eliminate any dominated and practically dominated alternatives (addresses), e.g. by drawing a line through them in the consequences table (Table 3 above).
A dominated alternative is an address that is worse on at least one criterion and no better on all the other criteria than another address. In Table 3, it can be seen that 15 Pleasant Point is dominated by 6 Yellow Brick Road (i.e. the former has less floor space, worse public transport and higher rent).
Also, if there are any other alternatives that, though not dominated (as above), are only a bit better on a particular criterion than another address, but you feel that this minor advantage is too small to offset its disadvantages on one or more of the other criteria, then they can be eliminated too.
For example, relative to 77 Sunshine Lane, 50 Heavenly Way has slightly more floor space (10 m2) but its public transport is worse and the rent is $1500 higher. You might easily conclude that, overall, the second address is worse than the first. If so, then 50 Heavenly Way is practically dominated and can be eliminated.
These two eliminated alternatives have been crossed-out in Table 3. The three remaining alternatives – see Table 4 below – each have some significant advantages and disadvantages relative to each other. The objective of the even-swap method is to trade them off against each other.
The method involves a series of even swaps (trade-offs) between the three alternatives based on a fundamental principle of decision-making: If all alternatives have the same rating on a given criterion (e.g. they all cost the same), then that criterion is irrelevant for choosing between the alternatives, and so it can be dropped.
For example, with reference to Table 4, if 77 Sunshine Lane had a floor space of 400 (instead of 550) then this criterion could be ignored for choosing between the three remaining addresses. But, of course, in reality this address has a floor space of 550.
The question to ask, therefore, is: For 77 Sunshine Lane, hypothetically speaking, how much of a reduction in monthly rent would be sufficient to compensate for a reduction of 150 m2 in floor space? Suppose, you answer: $1500.
Thus, as the name of the even-swap method implies, an even swap decreases the value of an alternative on one criterion (e.g. floor space) while simultaneously increasing its value by an equivalent amount on another criterion (e.g. rent): here, $1500 less rent is an even swap for 150 m2 less floor space. (Clearly, the even-swap method makes use of pairwise comparisons, like the other methods discussed in this article.)
The effects of these two imaginary changes (even swaps) are recorded in square brackets in Table 4. Because all three addresses are now the same on the floor space criterion, this criterion can be ignored (eliminated).
With the objective of culling the criteria further, another trade-off worthwhile posing is between public transport and rent for 6 Yellow Brick Road: If public transport was high quality (instead of medium), what is the maximum monthly rent you would be willing to pay (instead of $5000)?
Suppose you answer (conveniently!): $6000. These two even swaps are also recorded in square brackets in Table 4. Thus, in addition to floor space, the public transport and rent criteria can be eliminated. After these three eliminations, the decision problem has simplified to the reduced form in the Table 5 below, with just two criteria left.
| Address | Floor space (m2) | Quality of work facilities | Quality of local amenities | Quality of public transport | Monthly rent ($) |
|---|---|---|---|---|---|
| 6 Yellow Brick Road | 400 | medium | medium | medium [high] | 5000 [6000] |
| 23 Happy Valley | 400 | high | low | high | 6000 |
| 77 Sunshine Lane | 550 [400] | low | medium | high | 7500 [6000] |
It can be seen in the Table 5 that 77 Sunshine Lane is dominated on the two remaining criteria by 6 Yellow Brick Road, and so this first address can be eliminated.
Ultimately, therefore, your decision comes down to choosing between 6 Yellow Brick Road and 23 Happy Valley with respect to which of the two ratings on the two criteria is preferred: medium, medium or high, low? (Notice that this – another pairwise comparison – is equivalent to the simplest possible form of Benjamin Franklin’s “moral or prudential algebra” above.)
| Address | Quality of work facilities | Quality of local amenities |
|---|---|---|
| 6 Yellow Brick Road | medium | medium |
| 23 Happy Valley | high | low |
As should be easily imaginable from working through this example, the even-swap method becomes increasingly unwieldy as the number of alternatives increases. The volume of even swaps and their possible permutations across the alternatives become increasingly difficult to keep track of and administer.
An obvious solution (a methodological extension) is to determine explicit weights for the criteria, representing their relative importance. The criteria and weights can then be applied to the alternatives to rank or choose between them.
The next three pairwise comparison methods are based on the explicit weighting of criteria. Because they are more algorithmically sophisticated than the manual methods above, they are implemented using specialized software, and so only overviews are offered here.
A great way to fully appreciate the methods’ power is by experiencing the software if you can, e.g. free trials of 1000minds’ PAPRIKA method are immediately available.
Analytic hierarchy process (AHP)
AHP (
Ratio scale measurements relate to the decision-maker’s judgments about how many more times important is one criterion or alternative relative to another criterion or alternative. These judgments are elicited using pairwise comparisons.
Thus, with respect to the relative importance of the criteria, AHP asks the decision-maker questions like this: “On a nine-point scale ranging from “equally preferred” (ratio = 1) to “extreme importance” (ratio = 9), how much more important to you is criterion 1 than criterion 2?”
For example (consistent with the illustration in the even-swap section above): “When choosing a new workplace, how much more important to you is Quality of work facilities than Quality of local amenities?”
If, for example, a person were to answer “very strongly important”, this corresponds to a relative-importance ratio of 7: meaning the first criterion is seven times more important than the second criterion.
All combinations of the criteria, two at a time, are pairwise compared in this way.
Similarly, the alternatives are scored relative to each other on each criterion in turn by pairwise comparing them using the same rating scale: e.g. “With respect to criterion 1, on a nine-point scale ranging from “equally preferred” (ratio = 1) to “extreme importance” (ratio = 9), how much more important to you is alternative A than alternative B?”
For example (continuing with the earlier even-swap illustration): “When thinking about the floor space criterion, how much more important to you is 77 Sunshine Lane (550 m2) than 6 Yellow Brick Road (400 m2)?”
If, for example, a person were to answer “moderately important”, this corresponds to a relative-importance ratio of 3: meaning the first alternative is three times more important than the second alternative.
All alternatives are pairwise compared on each criterion in this way.
From the decision-maker’s ratio scale measurements, the weights on the criteria and the scores for the alternatives on each criterion are calculated (using eigenvalue analysis). Applying the weights on the criteria and the scores for the alternatives results in the alternatives being ranked overall.
A comprehensive overview of AHP is available, including a worked example to demystify the process summarized above.
Cognitive difficulty of AHP
Most people find it cognitively difficult to represent the intensity of their preferences using ratio scale measurements. Expressing how strongly you feel about one criterion or alternative relative to another on a nine-point scale ranging from “equally preferred” (ratio = 1) to “extreme importance” (ratio = 9) is not a natural human mental activity.
In contrast, pairwise ranking – simply choosing one thing from two, without having to pay attention to the intensity of the difference between them – is a natural activity that everyone has experience of in their daily lives. We all make such judgments dozens, if not hundreds, of times every day. For example: Would you like a cup of coffee or tea? A beer or a wine? Is today warmer or cooler than yesterday? And so on.
This simplicity and naturalness of pairwise ranking means it is a more valid and reliable approach than AHP’s reliance on ratio-scale measurements of preferences.
“The advantage of choice-based methods is that choosing [in its simplest form,
pairwise ranking], unlike scaling, is a natural human task at which we all have
considerable experience, and furthermore it is observable and verifiable”
(
A short survey of other criticisms of AHP is available in
We round out our discussion of pairwise comparison methods with two other prominent pairwise ranking methods based on explicit weighting: Conjoint analysis or discrete choice experiments (DCE) and 1000minds’ PAPRIKA method.
Conjoint analysis or discrete choice experiments (DCE)
Conjoint analysis is a survey-based methodology widely used in market research, new product design, government policy-making and the social sciences to understand people’s preferences, and to shape products and policies accordingly.
In brief (a more detailed guide is
available here),
a conjoint analysis involves survey participants expressing their preferences by
repeatedly choosing from choice sets consisting of two or more hypothetical
alternatives at a time. A conjoint analysis is also known as a discrete choice
experiment (DCE) (
All conjoint analysis methods involve pairwise comparisons, and can be differentiated with respect to how many hypothetical alternatives are included in the choice sets presented to survey participants: typically, ranging from two to five alternatives at a time.
For methods based on choice sets with just two alternatives at a time, survey participants are asked to pairwise rank them, i.e. choose the “better” alternative.
For methods based on choice sets with three alternatives at a time, participants are asked to rank them overall (1st, 2nd, 3rd). Albeit three alternatives are included, in the process of ranking them, most people are likely to compare them in a pairwise fashion: e.g. “Do I like alternative A more or less than B, and more or less than alternative C? And how do I feel about B versus C?”
For methods based on choice sets with four or five alternatives at a time, participants
are asked to select just the “best” and “worst” alternatives – known as best-worst scaling
(
The advantage of choice sets with two alternatives at a time is that choosing between just two alternatives is the simplest possible choice (i.e. compared to ranking or choosing from three or more alternatives). This simplicity ensures that participants can make their choices with greater confidence (and faster), leading to survey results that more accurately reflect participants’ true preferences.
The pairwise ranking task can be simplified even more by defining each hypothetical alternative included in a choice set on just two attributes (or criteria) at a time. This type of conjoint analysis is known as partial-profile conjoint analysis.
In contrast, full-profile conjoint analysis is based on choice sets where the alternatives are defined on all attributes together at a time (e.g. six or more). Examples of partial- and full-profile choice sets respectively appear in Figures 1 and 2 below (for a conjoint analysis into smartphones).
Pairwise ranking full-profile choice sets is more cognitively difficult (and slower) than pairwise ranking partial-profile choice sets. Therefore, all else being equal, conjoint analysis results obtained using full-profiles are less likely to be accurate, albeit such choice sets are arguably more realistic.
When conjoint analysis surveys are implemented, sub-samples of participants are usually presented with common choice sets (e.g. a dozen or more) because of the huge number of choice sets that are possible, drawn from all possible pairs of all hypothetically possible alternatives defined on the attributes – of which there are billions of pairs!
Regression techniques (e.g. multinomial logit analysis and hierarchical Bayes estimation)
are applied to participants’ rankings of their choice sets to generate weights (sometimes
known as utilities or part-worths), representing the relative importance of the
attributes. These techniques are explained in detail in
These weights can then be used to shape product or policy design, as well as to influence other decisions.
1000minds’ PAPRIKA method
Implemented by
1000minds software,
the PAPRIKA method – an acronym for Potentially All
Pairwise RanKings of all possible
Alternatives (
PAPRIKA involves the decision-maker being asked a series of simple pairwise ranking questions based on choosing between two hypothetical alternatives defined on just two criteria (or attributes) at a time and involving a trade-off (in effect, the other criteria are the same). An example of a pairwise ranking question – involving choosing a car – appears in Figure 3 below.
Thus, PAPRIKA’s pairwise ranking questions are based on partial-profiles – just two criteria at a time – in contrast to full-profile methods which involve all criteria together at a time (e.g. six or more). The obvious advantage of such simple questions is that they are the easiest possible question to think about, and so decision-makers can answer them with more confidence (and faster) than more complicated questions.
It’s possible for the decision-maker to proceed to the “next level” of pairwise ranking questions, involving three criteria at a time, and then four, five, etc (up to the number of criteria included). But for most practical purposes answering questions involving just two criteria at a time is usually sufficient with respect to the accuracy of the results achieved.
Each time a decision-maker answers a pairwise ranking question, PAPRIKA adapts by applying the logical property of transitivity discussed earlier. For example, if the person ranks alternative A over B and then B over C, then, logically – by transitivity! – A must be ranked over C, and so a question about this third pair is not asked. PAPRIKA ranks this third pair implicitly, and any other pairwise rankings similarly implied by transitivity, and eliminates them, so that the decision-maker is not burdened by being asked any redundant questions.
Also, each time the decision-maker answers a pairwise ranking question, the method adapts with respect to the next question asked (one whose answer is not implied by earlier answers) by taking all preceding answers into account. Thus, PAPRIKA is also recognized as being a type of adaptive conjoint analysis or discrete choice experiment (DCE).
In the process of answering a relatively small number of questions, the decision-maker ends up having pairwise ranked all hypothetical alternatives defined on two criteria at a time, either explicitly or implicitly (by transitivity). Because the pairwise rankings are consistent, a complete overall ranking of alternatives is defined, based on the decision-maker’s preferences.
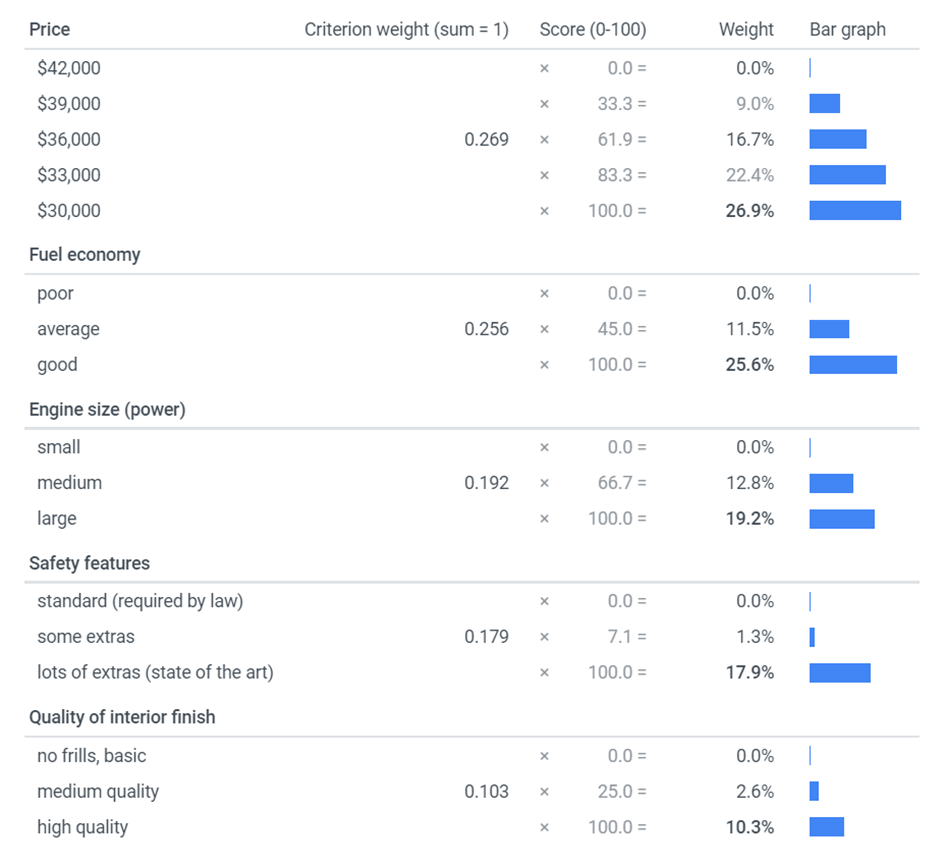
Finally, from the decision-maker’s pairwise rankings, mathematical methods are used to calculate the weights on the criteria, representing their relative importance. (In conjoint analysis, weights are also known as part-worths or utilities, as discussed above and below.)
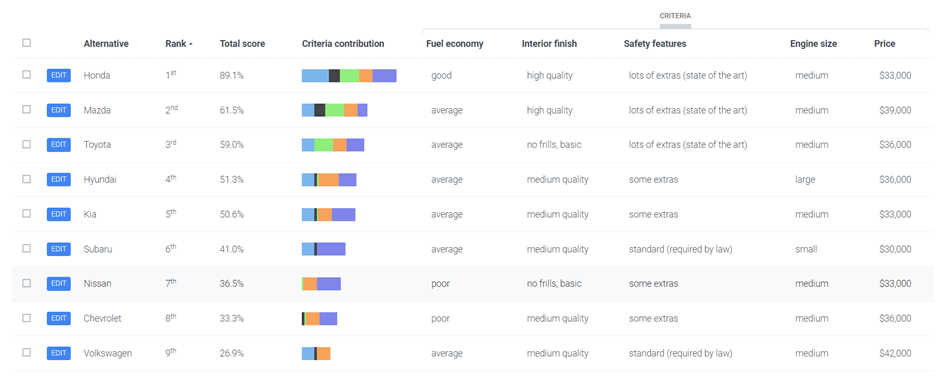
These weights are used to rank any alternatives being considered, or, depending on the application, all hypothetically possible alternatives (all combinations of the criteria). An example of a set of weights and ranked alternatives (cars) appears in Figures 4 and 5 below.
More detailed information about the PAPRIKA method is available here.
PAPRIKA for decision-making
The outputs from the pairwise ranking questions, as above, facilitate valid and reliable decision-making when many criteria are involved or a lot is at stake. For example, PAPRIKA can be used to make decisions about project management, prioritization of patients in hospitals, research grants, new job hires, or any other areas.
By reducing otherwise complex decisions down to answering the simplest possible pairwise ranking questions – choosing between two alternatives defined on just two criteria at a time – the decision-making process is made as easy as possible, thereby increasing reliability and repeatability.
Furthermore, 1000minds facilitates group decision-making by enabling people to vote on the pairwise ranking questions and to discuss them if need be, and hence to make decisions together as a team. Such an inclusive and participatory process encourages mutual understanding and group consensus.
PAPRIKA for conjoint analysis
PAPRIKA is also often used for conjoint analysis, for market research, new product design, government policy-making and social sciences research to understand people’s preferences, and to shape products and policies accordingly.
Using PAPRIKA, consumers or other stakeholders – e.g. citizens, policy-makers, clinicians, etc, depending on the application – answer a series of simple pairwise ranking questions, as above, to express their preferences. Their preferences are summarized as weights representing the relative importance of the attributes associated with the objects of interest.
These weights, or part-worths or utilities, can be analyzed directly or used to rank the alternatives being considered. See an example of a conjoint analysis and outputs derived using PAPRIKA to learn more.
Want to make smarter decisions using pairwise comparisons? Try 1000minds!
Step up your decision-making and conjoint analysis (or DCE) skills with 1000minds, which uses pairwise comparisons to make decisions consistently, fairly and transparently. Try a free 15-day trial today, or book a free demo to see how 1000minds can help you achieve your goals.
References
V Belton & T Stewart (2002), Multiple Criteria Decision Analysis: An Integrated Approach, Kluwer
J-C de Borda (1781), “Mémoire sur les élections au Scrutin”, Histoire de l’Academie Royale des Sciences, Paris
Marquis de Condorcet (1785), “Essai sur l’application de l’analyse à la probabilité des decisions rendues à la pluralité des voix”, Paris
M Drummond, M Sculpher, G Torrance, B O’Brien & G Stoddart (2015), Methods for the Economic Evaluation of Health Care Programmes, Oxford University Press
B Franklin (1772), “From Benjamin Franklin to Joseph Priestley, 19 September 1772”, In: Founders Online, National Historical Publications and Records Commission (NHPRC)
B Franklin (1772), Handwritten draft of letter from Benjamin Franklin to Joseph Priestley, September 19, 1772, Image 7 of Benjamin Franklin Papers: Series I, 1772-1783; Craven Street letterbook, London, England, 1772-1773 (vol. 11)
J Hammond, R Keeney & H Raiffa (1998), “Even swaps: A rational method for making trade-offs”, Harvard Business Review 76, 137-49
P Hansen & F Ombler (2008), “A new method for scoring multi-attribute value models using pairwise rankings of alternatives”, Journal of Multi-Criteria Decision Analysis 15, 87-107
R Keeney & H Raiffa (1976), Decisions with Multiple Objectives: Preferences and Value Tradeoffs, Cambridge University Press
J Louviere, T Flynn & A Marley (2015), Best-Worst Scaling: Theory, Methods and Applications, Cambridge University Press
D McFadden (1974), “Conditional logit analysis of qualitative choice behavior”, Chapter 4 in: P Zarembka (editor), Frontiers in Econometrics, Academic Press
T Saaty (1977), “A scaling method for priorities in hierarchical structures”, Journal of Mathematical Psychology 15, 234-81
K Train (2009), Discrete Choice Methods with Simulation, Cambridge University Press